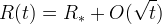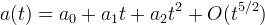Upgrade status: done. Please alert the webmaster about any anomalies.

You are here: Foswiki>Cosmo Web>GrassmannCosmoFun2009>GrassCosmoFun09Fri (18 Sep 2009, BoudRoukema)Edit Attach

Fri 18 Sep 2009

main page: GrassmannCosmoFun2009

These are just rough notes - feel free to correct them, add links, etc. from the Grassmann ian Conference in Fundamental Cosmology (Grasscosmofun'09). These are not official proceedings. The speakers might even disagree that they said anything even vaguely related to what are in these online notes! Don't say you weren't warned.

Fri 18 Sep 2009

STAROBINSKY - f(R) models

particle content: graviton +
- massive scalar particle ( M^2 = 1/{3 f''(R)} ) (called "scalaron" in Starobinsky 1980)
stability conditions:
- f' > 0 graviton is not a ghost * f'' > 0 scalaron is not a tachyon
imposed for R \ge R_{now} at least (i.e. during the whole evolution of the Universe)
possible microscopic origin of f(R) gravity
- vacuum polarisation in curved space-time
- reduction to 4D from curved (4+n)-D space-time
- limiting case of scalar-tensor gravity
- emergent gravity Klinkhamer & Volovik (2008) ArXiv:0807.3896
violation of these conditions is undesirable also from the classical point of view
- f'(R_*) = 0 instant loss of homogeneity and isotropy
- f''(R_*) = 0 weak singularity
  - $R(t) = R_* + O(\sqrt{t})$
  - $a(t) = a_0 + a_1 t + a_2 t^2 + O(t^{5/2})$
existence of the Newtonian regime $\Delta(\phi) = 4 \pi G \rho$
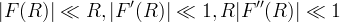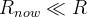- $|F(R)| \ll R, |F'(R)| \ll 1, R |F''(R)| \ll 1$ for $R_{now} \ll R$ (up to some very large R)
- de Sitter regime 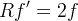stable if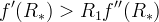
- equivalent to 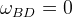$\omega_{BD} = 0$ in scalar-tensor gravity
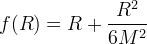
use for inflation Starobinsky 1980: $f(R) = R + \frac{R^2}{6 M^2}$
- internally consistent infolationary model with slow-roll decay, a graceful exit to the subsequent RD (radiation-dominated) FRW stage ... and sufficiently effective reheating
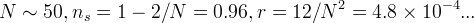
- model remains viable, e.g. $N \sim 50, n_s = 1 - 2/N = 0.96, r = 12/N^2 = 4.8 \times 10^{-4} ...$
oher viable f(R) inflationary models
- 1. chaotic type - inflation over a large range of R
- 2. new inflationary type - inflation around R =R_0
- both cases: f(R) close to R^2/{6M^2}
viable for DE???
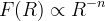- $F(R) \propto R^{-n}$ for $R \rightarrow 0$ does not work for many reasons
- viable model - must be regular at $=0
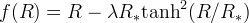  - Starobinsky 2007, ArXiv:0706.2041 : $f(R) = R + \lambda R_* \left[\frac{1}{ \left( 1 + R^2/R_*^(?) \right)^n} -1 \right]$ * or: $f(R) = R - \lambda R_* \mathrm{tanh}^2 (R/R_*)$ * f(0) = 0
observational constraints
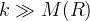
- cosmology - anomalous growth of non-relativistic matter perturbations in the regime $k \gg M(R)$
- lab and Solar System tests 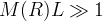$M(R) L \gg 1$ with R = 8 pi G T_m = 8 \pi G \rho_m; otherwise, \gamma_{(?)} = 1/2 and 'fifth' force appears
- both OK if n \ge 2
... "scalaron production" problems
"big boost" singularity with $R \rightarrow \infty$ and its elimination
- elimination: add R^2/{6M^2} to F(R)
conclusions:
- viable models of DE, distinguishable from LambdaCDM, exist, given certain conditions:
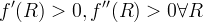
  - with a regular f(R) satisfying: $f'(R) > 0, f''(R) > 0 \forall R$
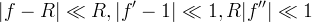  - $|f-R| \ll R, |f'-1| \ll 1, R|f''| \ll 1$ * ...
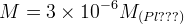
- unification of primordial DE (i.e. inflation) and present DE is possible for $M = 3\times 10^{-6} M_{(Pl???)}$
- anomalous growth of scalar perturbations at recent times ( z about 1-3 for L = 8 /h Mpc ) would be the most critical test of the f(R) DE models satisfying these conditions

David POLARSKI - DE

scalar-tensor theories AstroPh:0701650, AstroPh:0507290
LambdaCDM problems?
- nbDM halo density profile - no cups seen?
- large scale peculiar flows
- unexpected brightness of SNe Ia at z > 1 (??)
- void problem
- w = -1 constant is an Achilles' heel
quintessence
Lagrangian L = fn(F(phi), R, Z U(phi), g_munu
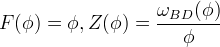Brans-Dicke parametrisation $F(\phi) = \phi, Z(\phi) = \frac{\omega_{BD}(\phi)}{\phi}$ ...
- $G_{\mathrm{eff}}, G_N, G_*$
effects on structure formation

Roman JUSZKIEWICZ

non-linear perturbation theory for sigma_8

Jerzy KROL

exotic R^4, QG and QFT - ArXiv:0904.1276 and references therein
- R^n with n=4 case is particularly difficult

Babak VAKILI

Noether approach ...

-- BoudRoukema - 18 Sep 2009

Attachments 22

I	Attachment	Action	Size	Date	Who
png	029b116344f4e7ce9bf06177965100cc.png	manage	577 bytes	18 Sep 2009 - 09:28	UnknownUser
png	0fcf96209d4c32599e44f4450ffb4523.png	manage	927 bytes	18 Sep 2009 - 09:28	UnknownUser
png	1f9f68708997697a443df1a36e690167.png	manage	714 bytes	18 Sep 2009 - 09:28	UnknownUser
png	21cc4271af5a0ec2c8981b9c2d15616a.png	manage	539 bytes	18 Sep 2009 - 09:28	UnknownUser
png	280db62aa760caef7f1c6772fe481d70.png	manage	426 bytes	18 Sep 2009 - 09:28	UnknownUser
png	2ea84b199112103c17a0573e11e12ca9.png	manage	685 bytes	18 Sep 2009 - 09:28	UnknownUser
png	3782d46380ee672df4ab155182e17f50.png	manage	457 bytes	18 Sep 2009 - 10:37	UnknownUser
png	3bff5e0dc63f47c4f8ac5a8b54942e28.png	manage	729 bytes	18 Sep 2009 - 09:28	UnknownUser
png	3d6d04299e6e62175cd3a7cf6914ad46.png	manage	334 bytes	18 Sep 2009 - 09:28	UnknownUser
png	6d0c36f39e8b26ae435b6f06a890f852.png	manage	310 bytes	18 Sep 2009 - 09:28	UnknownUser
png	7624981ab1ded3569199a8ab71a5d14a.png	manage	839 bytes	18 Sep 2009 - 10:27	UnknownUser
png	77bcec14092334e90ad05c907d547cb0.png	manage	465 bytes	18 Sep 2009 - 09:28	UnknownUser
png	848d5153ae0a119b20f8694e5b005a7a.png	manage	1 K	18 Sep 2009 - 09:28	UnknownUser
png	9e9935fa02de755f3ae2046dcbf2796d.png	manage	558 bytes	18 Sep 2009 - 09:28	UnknownUser
png	bb4322e6607f68e78d3558a9ad51e744.png	manage	1 K	18 Sep 2009 - 09:28	UnknownUser
png	beb56b660411062c6b3d7e17eec61848.png	manage	1 K	18 Sep 2009 - 09:28	UnknownUser
png	c0e5bf790dfb0819ebb5e2ad32037b95.png	manage	368 bytes	18 Sep 2009 - 09:28	UnknownUser
png	c9e6369b20d0b854f48145975c419a15.png	manage	804 bytes	18 Sep 2009 - 09:28	UnknownUser
png	cddf2a84de02ce165ab060af234306f2.png	manage	545 bytes	18 Sep 2009 - 09:28	UnknownUser
png	cfa9818ec7491c4c4837c0bf5a0ab263.png	manage	702 bytes	18 Sep 2009 - 09:28	UnknownUser
png	d2ec837bb857936da7b7360448768d17.png	manage	926 bytes	18 Sep 2009 - 09:28	UnknownUser
png	df3372c6349f8fdb39ee3b21501acf44.png	manage	869 bytes	18 Sep 2009 - 09:28	UnknownUser

Topic revision: r2 - 18 Sep 2009, BoudRoukema

Cosmo

Webs
Cosmo
Main
Sandbox

Copyright © by the contributing authors. All material on this collaboration platform is the property of the contributing authors.
Ideas, requests, problems regarding Foswiki? Send feedback