OEF bilinéaires --- Introduction ---

Ce module regroupe pour l'instant 10 exercices sur les formes bilinéaires et formes quadratiques.

Base de vecteurs propres

Soit la forme quadratique définie, pour , par

.

La matrice associée à dans la base canonique est :
Entrer la matrice ligne par ligne, les coefficients d'une même ligne sont séparés par des virgules. La matrice de dans la base canonique est bien .

L'ensemble des valeurs propres de la matrice est . Les valeurs propres de la matrice sont bien .

Donner une base orthogonale par rapport à Q et orthonormée par rapport au produit scalaire usuel de .

Entrer en colonne les composantes des vecteurs de la base , séparées par des virgules.

Formes bilinéaires

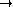
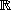Soit times to RR l'application définie par

avec et .

L'application est-elle une forme bilinéaire symétrique ?

Formes bilinéaires, formes quadratiques

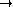
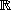Soit to RR la forme quadratique suivante :

.
Déterminer parmi les choix suivants l'unique forme bilinéaire symétrique times to RR telle que pour tout dans .

Formes bilinéaires et matrices

Pour rentrer la matrice, écrire les coefficients ligne par ligne : les coefficients d'une même ligne sont séparés par des virgules.

Invariants d'une conique

Soit la conique

.

Soit .

La forme quadratique est-elle ou Déterminer le centre de la conique et le réel tel que

Ainsi dans le repère affine dont l'origine est le centre ( , ) de la conique, la conique a comme équation

Déterminer la signature de . Une des valeurs propres de est 0. Calculer la seconde valeur propre et donner une base de vecteurs propres vérifiant les conditions suivantes : Soient les coordonnées dans la base ( , ). Déterminer et pour que

.

La conique a comme équation .

Quelle est la nature de la conique ?

Formes quadratiques équivalentes

Soit la forme quadratique définie, pour , par

Indiquer laquelle des formes quadratiques suivantes est équivalente à

    • Rang d'une forme quadratique

    Soit , la forme quadratique définie pour par

    La signature de Q est et son rang vaut .
    Voici la matrice de sous forme utilisable dans les outils : .

    Réduction de Gauss

    Soit la forme quadratique définie pour par

    Déterminer une décomposition de Gauss de
    Entrer les formes linéaires en ligne en séparant les coefficients d'une même ligne par des virgules :

    Entrer les dans le même ordre, séparés par des virgules :

    Signature d'une forme quadratique

    Soit , la forme quadratique définie pour par

    1. Déterminer les valeurs propres de la matrice associée à .
    2. Calculer sa signature de Q.
    Voici la matrice de sous forme utilisable dans les outils : .

    Signature et rang

    Soit une forme quadratique sur .

    La signature de est et son rang vaut The most recent version

    Cette page n'est pas dans son apparence habituelle parce que WIMS n'a pas pu reconnaître votre navigateur de web.

    Pour accéder aux services de WIMS, vous avez besoin d'un navigateur qui connait les formes. Afin de tester le navigateur que vous utilisez, veuillez taper le mot wims ici : puis appuyez sur ``Entrer''.

    Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.

    Description: collection d'exercices sur les formes bilinéaires et formes quadratiques. interactive exercises, online calculators and plotters, mathematical recreation and games

    Keywords: interactive mathematics, interactive math, server side interactivity, algebra, bilinéaire, quadratique,forme,dégénérée,rang, signature